Periodic boundary conditions

Periodic boundary conditions#

boundary value problem on \(\textbf{x}\in\Omega\)

\[\nabla^2 u = f(\textbf{x})\]

Neumann boundary condition on \(\textbf{x}\in\partial\Omega_{\text{D}}\)

\[u = u_{\text{D}}\]

Neumann boundary condition on \(\textbf{x}\in\partial\Omega_{\text{N}}\)

\[\textbf{n}\cdot\nabla u = u_{\text{N}}\]

periodic boundary condition on \(\textbf{x}\in\partial\Omega_{\text{M}}\cup\in\partial\Omega_{\text{S}}\)

\[u\vert_{\partial\Omega_{\text{M}}} = u\vert_{\partial\Omega_{\text{S}}}\]
import numpy as np
from dolfinx.fem import FunctionSpace

from lucifex.mesh import rectangle_mesh, mesh_boundary
from lucifex.fem import Function
from lucifex.solver import bvp, BoundaryConditions, OptionsPETSc
from lucifex.viz import plot_colormap, plot_line
from lucifex.utils import cross_section

from lucifex.pde.poisson import poisson


Lx = 2.0
Ly = 1.0
mesh = rectangle_mesh(Lx, Ly, 64, 64)
boundary = mesh_boundary(
    mesh, 
    {
        "left": lambda x: x[0],
        "right": lambda x: x[0] - Lx,
        "lower": lambda x: x[1],
        "upper": lambda x: x[1] - Ly,
    },
)

def right_to_left(x: np.ndarray) -> np.ndarray:
    return np.vstack((x[0] - Lx, x[1]))

def upper_to_lower(x: np.ndarray) -> np.ndarray:
    return np.vstack((x[0], x[1] - Ly))

fs = FunctionSpace(mesh, ('P', 1))

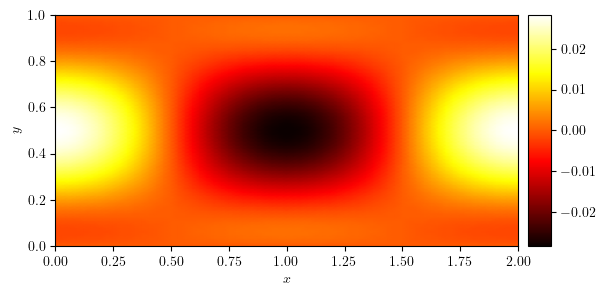
Periodic in the \(x\)-direction (\(\partial\Omega_{\text{D}}\cup\partial\Omega_{\text{N}}\neq\varnothing\))#

\[c(x=0,y)=c(x=L_x,y)\]
\[c(x,y=0)=c(x,y=L_y)=0\]
bcs_pbc_x = BoundaryConditions(
    ('periodic', boundary['right'], right_to_left),
    ("dirichlet", boundary['lower', 'upper'], 0.0),
)
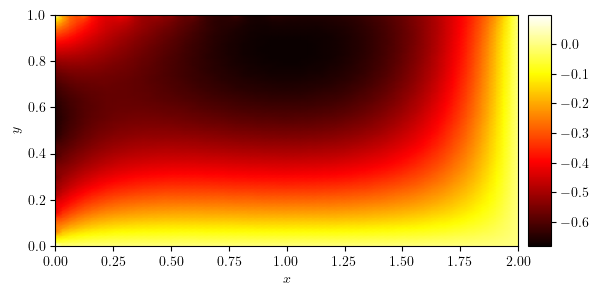
f = Function(fs, lambda x: np.cos(2 * np.pi * x[0] / Lx) * np.cos(2 * np.pi * x[1] / Ly), name='f')
u = Function(fs, name='u')
u_solver = bvp(poisson, bcs_pbc_x)(u, f)
u_solver.solve()

plot_colormap(u)

(<Figure size 640x480 with 2 Axes>, <Axes: xlabel='$x$', ylabel='$y$'>)
../../_images/8c6025790b3f0322c140b24f2ca3331db9098ed2bb9615c38f055b2eb457e348.png 
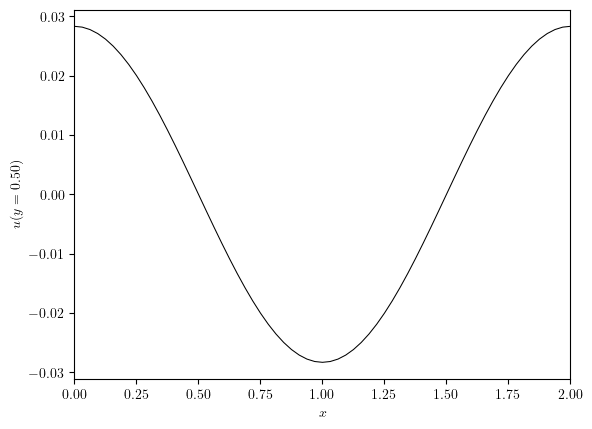
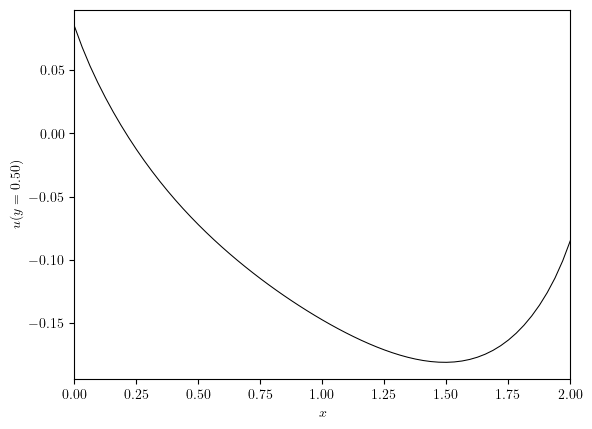
x_axis, ux, y_value = cross_section(u, 'y', 0.5)
plot_line((x_axis, ux), x_label='$x$', y_label=f'${u.name}(y={y_value:.2f})$')

(<Figure size 640x480 with 1 Axes>, <Axes: xlabel='$x$', ylabel='$u(y=0.50)$'>)
../../_images/1f567548013e4d4693225164320cd15728ff4abc3810b5186d472b6601ca677e.png

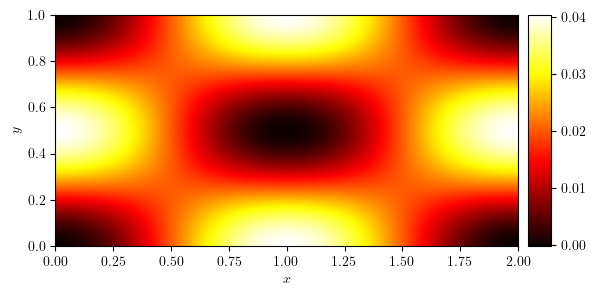
Periodic in the \(x\) and \(y\) directions (\(\partial\Omega_{\text{D}}\cup\partial\Omega_{\text{N}}=\varnothing\))#

\[c(x=0,y)=c(x=L_x,y)\]
\[c(x,y=0)=c(x,y=L_y)\]
bcs = BoundaryConditions(
    ('periodic', boundary['upper'], upper_to_lower),
    ('periodic', boundary['right'], right_to_left),
)

u = Function(fs, name='u')
f = Function(fs, lambda x: np.cos(2 * np.pi * x[0] / Lx) * np.cos(2 * np.pi * x[1] / Ly), name='f')
u_solver = bvp(poisson, bcs)(u, f)
u_solver.solve()

plot_colormap(u)

(<Figure size 640x480 with 2 Axes>, <Axes: xlabel='$x$', ylabel='$y$'>)
../../_images/e420626579a9844a3b53dfa2739460a0818fddf9b81397c61d4a91f5de4ab441.png

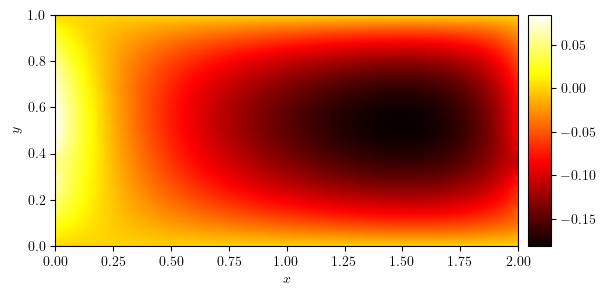
Antiperiodic in the \(x\)-direction#

\[c(x=0,y)=-c(x=L_x,y)\]
\[c(x,y=0)=c(x,y=L_y)=0\]
bcs = BoundaryConditions(
    ('antiperiodic', boundary['right'], right_to_left),
    ("dirichlet", boundary['lower', 'upper'], 0.0),
)
f = Function(fs, lambda x: x[0] + x[1] ** 2, name='f')
u = Function(fs, name='u')
u_solver = bvp(poisson, bcs)(u, f)
u_solver.solve()

plot_colormap(u)

(<Figure size 640x480 with 2 Axes>, <Axes: xlabel='$x$', ylabel='$y$'>)
../../_images/6ee35699275c96066da8e04e0a9ee576ebe907ef6c61b11fadb7713e1009ebbe.png 
x_axis, ux, y_value = cross_section(u, 'y', 0.5)
plot_line((x_axis, ux), x_label='$x$', y_label=f'${u.name}(y={y_value:.2f})$')

(<Figure size 640x480 with 1 Axes>, <Axes: xlabel='$x$', ylabel='$u(y=0.50)$'>)
../../_images/b635b0dc693b4629ec934f927712e13b7ba247e739e0eb63dba6a65dcd007a8c.png

Cross-periodicity#

\[c(x,y=L_y)=c(x=0,y)\]
\[c(x=0,y)=c(x=L_x,y)=0\]
def upper_to_left(x: np.ndarray) -> np.ndarray:
    return np.vstack((np.zeros_like(x[0]), (Ly / Lx) * x[0]))


f = Function(fs, lambda x: 1.0 + x[0] + x[1] ** 2, name='f')

bcs = BoundaryConditions(
    ('periodic', boundary['upper'], upper_to_left),
    ('dirichlet', boundary['right', 'lower'], 0.0),
)

u = Function(fs, name='u')

petsc = OptionsPETSc('preonly', 'lu', 1e-12, 1e-14)
u_solver = bvp(poisson, bcs, petsc)(u, f)
u_solver.solve()

plot_colormap(u, use_cache=False)

(<Figure size 640x480 with 2 Axes>, <Axes: xlabel='$x$', ylabel='$y$'>)
../../_images/86dbc296467a1f67b434e23c99a84da7334acdcbc34d15d2a8a9b0fd235cb8e4.png 
The Kernel crashed while executing code in the current cell or a previous cell. 

Please review the code in the cell(s) to identify a possible cause of the failure. 

Click <a href='https://aka.ms/vscodeJupyterKernelCrash'>here</a> for more info. 

View Jupyter <a href='command:jupyter.viewOutput'>log</a> for further details.
Contents