Marangoni convection of a Navier-Stokes fluid in a rectangle

\[\begin{split} \mathbb{S} \begin{cases} \Omega = [0, \mathcal{A}X] \times [0, X] & \text{aspect ratio } \mathcal{A}=\mathcal{O}(1) \\ \textbf{e}_g=-\textbf{e}_y & \text{vertically downward gravity} \\ c_0(x,y)=\text{exp}\left(-\frac{(y-h)^2}{\epsilon}\right) + \mathcal{N}(x,y) \\ \textbf{u}_0=\textbf{0} & \text{static initial conditions} \\ p_0=0 \\ c_{\text{N}}\vert_{\partial\Omega}=0 & \text{no-flux on entire boundary} \\ (\textbf{n}\cdot\textbf{u})\vert_{x, y=1}=0 & \text{no-penetration on upper boundary} \\ \boldsymbol{\tau}_{\text{N}}(x,y=1) = -Ma\frac{\partial c}{\partial x}\textbf{e}_x & \text{Marangoni stress on upper boundary} \\ \textbf{u}_{\text{E}}(x=0, y)=\textbf{0} & \text{no-flow on left boundary} \\ \textbf{u}_{\text{E}}(x=L_x, y)=\textbf{0} & \text{no-flow on right boundary} \\ \textbf{u}_{\text{E}}(x, y=0)=\textbf{0} & \text{no-flow on lower boundary} \\ \rho(c)=c & \text {linear density} \\ \mu=1 & \text {constant viscosity} \\ \tau(\textbf{u})=\tfrac{1}{2}(\nabla\textbf{u} + (\nabla\textbf{u})^{\mathsf{T}}) & \text{Newtonian stress} \\ \end{cases} \end{split}\]

from lucifex.sim import run
from lucifex.solver import maximum, minimum
from lucifex.viz import plot_colormap, plot_streamlines, plot_line, plot_stacked_lines, save_figure
from lucifex.utils import get_component_fem_functions, as_indices
from py.C03_navier_stokes_marangoni import navier_stokes_marangoni

simulation = navier_stokes_marangoni(
    aspect=2.0,  
    Nx=64,
    Ny=64,
    cell='quadrilateral',
    Ra=1e2,
    Pr=1e1,
    Ma=1e4,
    c_ampl=1e-3,
    c_freq=(16, 8),
    dt_max=0.01, 
)

n_stop = 50
dt_init = 1e-6
n_init = 10
run(simulation, n_stop=n_stop, dt_init=dt_init, n_init=n_init)

c, u = simulation['c', 'u']

i_thumb =  0.25
time_indices = as_indices(c.time_series, (0, i_thumb, 0.5, 0.75, -1), fraction=True)
for i in time_indices:
    cn = c.series[i]
    tn = c.time_series[i]
    un = u.series[i]
    ux, uy = get_component_fem_functions(('P', 1), un, names=('ux', 'uy'))
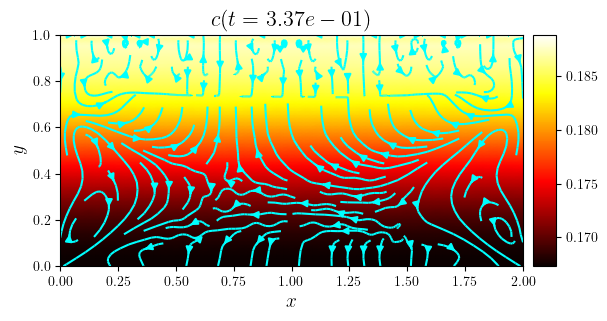
    fig, ax = plot_colormap(cn, title=f'$c(t={tn:.2e})$')
    plot_streamlines(fig, ax, (ux, uy), color='cyan')
    save_figure(f'c(x,y,t={tn})_streamlines', thumbnail=(i == i_thumb))(fig)

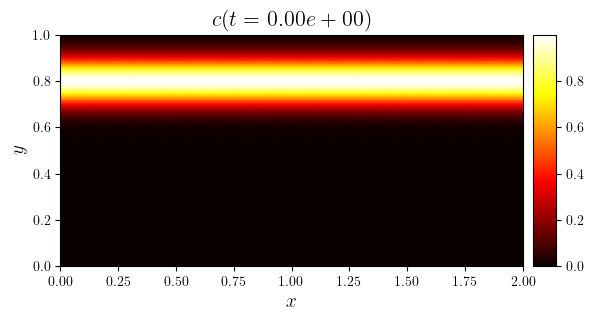
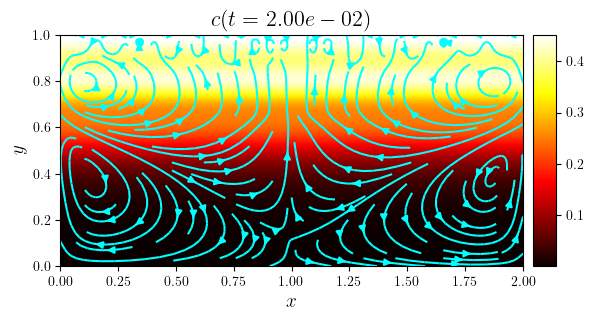
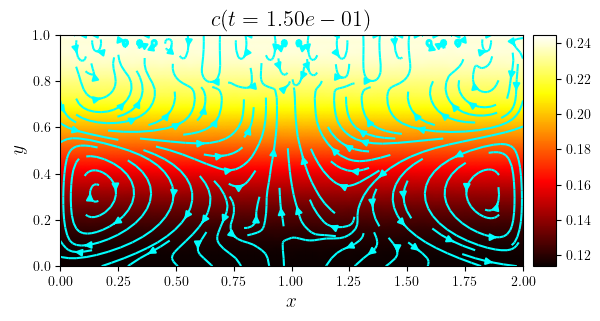
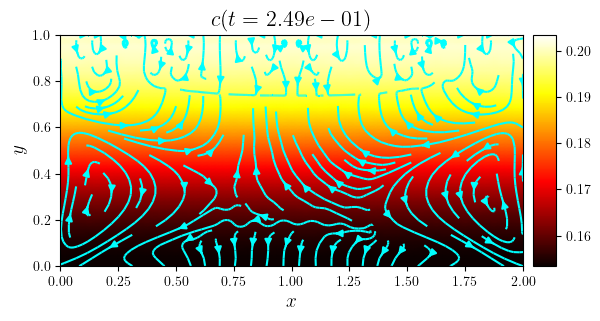
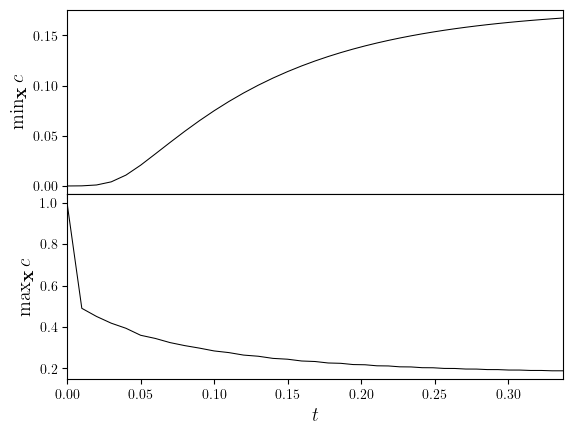
c_min = [minimum(i) for i in c.series]
c_max = [maximum(i) for i in c.series]

fig, ax = plot_stacked_lines(
    [(c.time_series, c_min), (c.time_series, c_max)],
    x_label='$t$',
    y_labels=['$\min_{\mathbf{x}}c$', '$\max_{\mathbf{x}}c$'],
)
save_figure(f'cMinMax(t)')(fig)

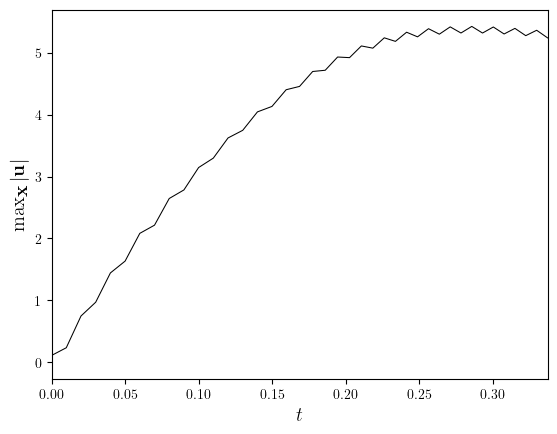
uMax = [maximum(i) for i in u.series]
fig, ax = plot_line((u.time_series, uMax), x_label='$t$', y_label='$\max_{\\textbf{x}}|\\textbf{u}|$')
save_figure(f'uMax(t)')(fig)

The Kernel crashed while executing code in the current cell or a previous cell. 

Please review the code in the cell(s) to identify a possible cause of the failure. 

Click <a href='https://aka.ms/vscodeJupyterKernelCrash'>here</a> for more info. 

View Jupyter <a href='command:jupyter.viewOutput'>log</a> for further details.