Rayleigh-Bénard convection of a Darcy fluid in a porous annulus

\[\begin{split} \mathbb{S} \begin{cases} \Omega = \Omega = \{(x, y)~:~(\mathcal{A}X)^2 < x^2 + y^2 < X^2\} & \text{aspect ratio } 0<\mathcal{A}<1 \\ \partial\Omega_{\text{inner}} = \{(x, y)~:~ x^2 + y^2 = (\mathcal{A}X)^2 \} \\ \partial\Omega_{\text{outer}} = \{(x, y)~:~ x^2 + y^2 = X^2 \} \\ \textbf{e}_g = -\frac{x}{\sqrt{x^2+y^2}}\textbf{e}_x -\frac{y}{\sqrt{x^2+y^2}}\textbf{e}_y & \text{radially inward gravity} \\ \mathsf{D} = \mathsf{I} & \text{constant isotropic dispersion}\\ \mathsf{K} = \mathsf{I} & \text{constant isotropic permeability}\\ \mu = 1 & \text{constant viscosity} \\ \rho(c) = -c & \text{linear density}\\ c_0(x,y)=\frac{\ln(X/\sqrt{x^2 + y^2})}{\ln(1/\mathcal{A})}+\mathcal{N}(x,y) & \text{perturbed diffusive base state} \\ c_{\text{D}}\vert_{\partial\Omega_{\text{inner}}}=1 & \text{`hot' inner boundary} \\ c_{\text{D}}\vert_{\partial\Omega_{\text{outer}}}=0 & \text{`cold' outer boundary} \\ \psi_{\text{D}}\vert_{\partial\Omega}=0 & \text{no-penetration on entire boundary} \end{cases} \end{split}\]

from lucifex.fdm import AB2, CN
from lucifex.sim import run
from lucifex.utils import triangulation, as_indices
from lucifex.viz import plot_colormap, plot_mesh, create_animation, save_figure, display_animation
from py.C01_darcy_rayleigh_benard import darcy_rayleigh_benard_annulus


simulation = darcy_rayleigh_benard_annulus(
    Rratio = 0.5,
    Nradial=32,
    scaling='advective',
    Ra=300.0, 
    c_ampl=1e-3,  
    c_freq=6, 
    D_adv=AB2,
    D_diff=CN,
)

n_stop = 200
dt_init = 1e-6
n_init = 5
run(simulation, n_stop=n_stop, dt_init=dt_init, n_init=n_init)

c = simulation['c']

time_slice = slice(0, None, 2)
titles = [f'$c(t={t:.3f})$' for t in c.time_series[time_slice]]

anim = create_animation(
    plot_colormap,
    colorbar=False,
)(c.series[time_slice], title=titles)
anim_path = save_figure('c(x,y,t)', get_path=True)(anim)

display_animation(anim_path)

mesh = c.function_space.mesh
mesh_tri = triangulation(mesh)
x, y = mesh_tri.x, mesh_tri.y

c_base, c_pert = c.ics_perturbation
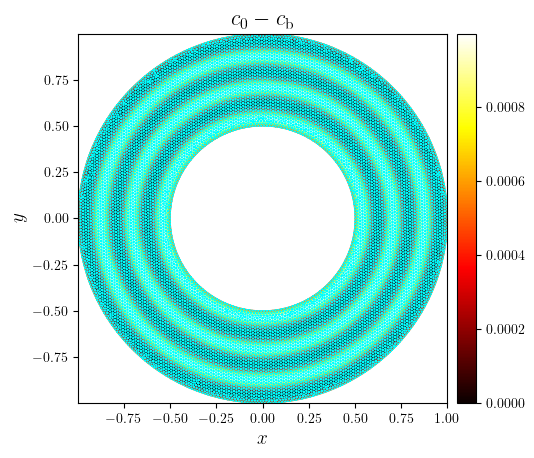
fig, ax = plot_colormap(
        (mesh_tri, triangulation(c_pert)), 
        title=f'$c_0 - c_{{\mathrm{{b}}}}$',
        cartesian=False, 
    )
plot_mesh(fig, ax, mesh, color='cyan', linewidth=0.5)
save_figure('noise(x,y)_mesh')(fig)

mesh = c.function_space.mesh
mesh_tri = triangulation(mesh)
x, y = mesh_tri.x, mesh_tri.y

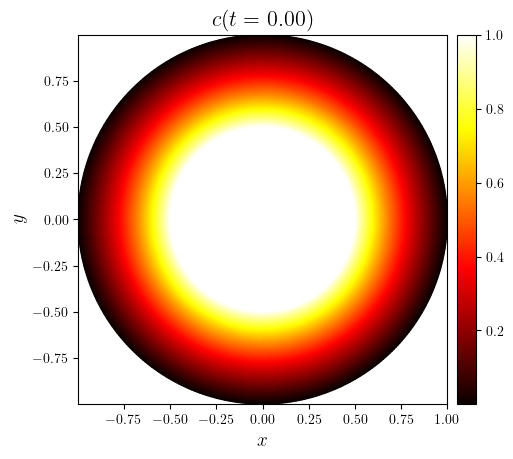
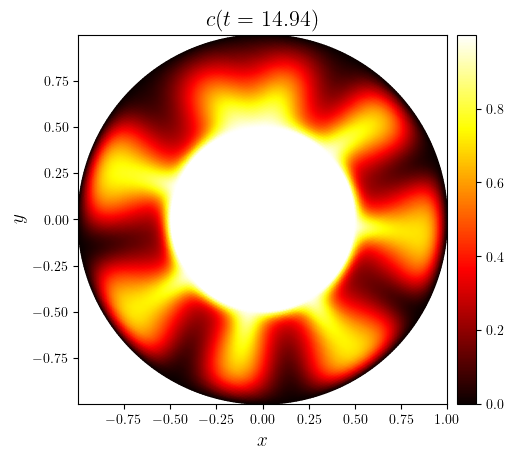
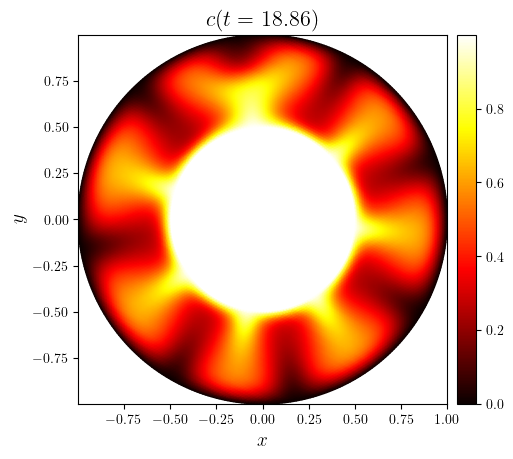
time_indices = as_indices(c.time_series, (0, 0.5, -1), fraction=True)
for i in time_indices:
    c_tri = triangulation(c.series[i])
    fig, ax = plot_colormap(
        (mesh_tri, c_tri), 
        title=f'$c(t={c.time_series[i]:.2f})$',
        cartesian=False, 
    )
    save_figure(f'c(x,y,t={c.time_series[i]:.2f})', thumbnail=(i == -1))(fig)

The Kernel crashed while executing code in the current cell or a previous cell. 

Please review the code in the cell(s) to identify a possible cause of the failure. 

Click <a href='https://aka.ms/vscodeJupyterKernelCrash'>here</a> for more info. 

View Jupyter <a href='command:jupyter.viewOutput'>log</a> for further details.