Flow of a Darcy fluid across an anticline of heterogeneous permeability

\[\begin{split} \mathbb{S}_{\psi} \begin{cases} \Omega = \{(x,y)~:~~R_{\text{inner}}^2 < x^2 + y^2 < R_{\text{outer}}^2~,~y>0\} \\ \partial\Omega_{\text{upper}} = \{(x,y)~:~x^2 + y^2 < R_{\text{outer}}^2\} \\ \partial\Omega_{\text{lower}} = \{(x,y)~:~x^2 + y^2 < R_{\text{inner}}^2\} \\ \partial\Omega_{\text{in}} = \{(x,y)~:~y=0~,~-R_{\text{outer}}<x<-R_{\text{inner}}\} \\ \partial\Omega_{\text{out}} = \{(x,y)~:~y=0~,~R_{\text{inner}}<x<R_{\text{outer}}\} \\ \mathsf{K}(\textbf{x})=\mathcal{N}(\textbf{x})\mathsf{I} & \text{random isotropic permeability} \\ \mu=1 \\ \psi_{\text{D}}\vert_{\partial\Omega_{\text{upper}}}=0 & \text{no-penetration on upper boundary}\\ \psi_{\text{D}}\vert_{\partial\Omega_{\text{in}}}=-u_{\text{in}}(x+R_{\text{outer}}) & \text{inflow boundary} \\ \psi_{\text{D}}\vert_{\partial\Omega_{\text{out}}}=u_{\text{in}}(x-R_{\text{outer}}) & \text{outflow boundary} \\ \psi_{\text{D}}\vert_{\partial\Omega_{\text{lower}}}=-u_{\text{in}}(R_{\text{outer}}-R_{\text{inner}}) & \text{no-penetration on lower boundary} \\ \end{cases} \end{split}\]

import numpy as np
from lucifex.fem import Function, Constant, DofsPerturbation
from lucifex.mesh import annulus_sector_mesh, mesh_boundary
from lucifex.solver import BoundaryConditions, bvp
from lucifex.viz import plot_contours, plot_mesh, plot_colormap, save_figure
from lucifex.pde.darcy import darcy_streamfunction


Rinner = 1.0
Router = 2.0
Nradial = 10
dr = (Router - Rinner) / Nradial
mesh = annulus_sector_mesh(dr, 'triangle', 'anticline')(Rinner, Router, 180)

r2 = lambda x: x[0]**2 + x[1]**2
boundary = mesh_boundary(
    mesh, 
    {
        "lower": lambda x: r2(x) - Rinner**2,
        "upper": lambda x: r2(x) - Router**2,
        "in": lambda x: np.logical_and(np.isclose(x[1], 0.0), x[0] < 0),
        "out": lambda x: np.logical_and(np.isclose(x[1], 0.0), x[0] > 0),
    },
)

mu = Constant(mesh, 1.0)
k_lims = (0.05, 1.0)
k_noise = DofsPerturbation(
    0.0,
    1234,
    k_lims,
    (16, 16)
)
k = k_noise.combine_base_noise((mesh, 'P', 1), name='k')

psi = Function((mesh, 'P', 2), name='psi')
u_in = 1.0
psi_bcs = BoundaryConditions(
    ('dirichlet', boundary['upper'], 0.0),
    ('dirichlet', boundary['in'], lambda x: -u_in * (x[0] + Router)),
    ('dirichlet', boundary['lower'], -u_in * (Router - Rinner)),
    ('dirichlet', boundary['out'], lambda x: u_in * (x[0] - Router)),
)
psi_solver = bvp(darcy_streamfunction, psi_bcs)(psi, k, mu)
psi_solver.solve()

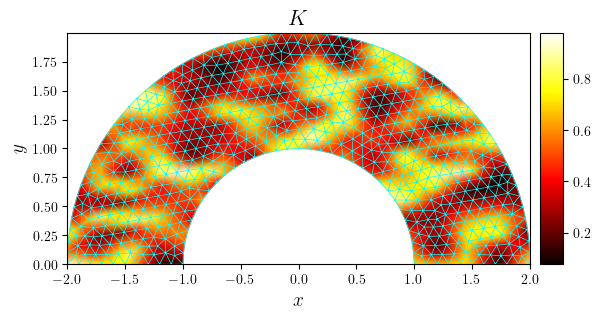
fig, ax = plot_colormap(k, title='$K$', x_label='$x$', y_label='$y$')
plot_mesh(fig, ax, mesh, color='cyan', linewidth=0.5)
save_figure('K(x,y)_mesh')(fig)

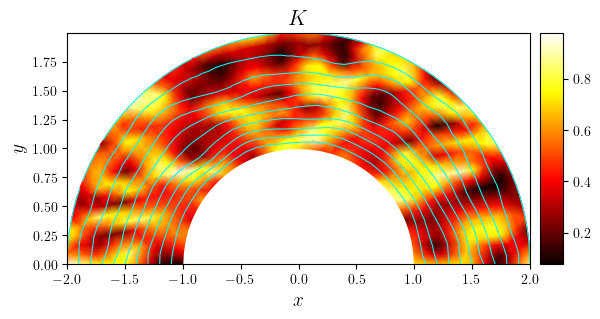
fig, ax = plot_colormap(k, title='$K$', x_label='$x$', y_label='$y$')
plot_contours(fig, ax, psi, colors='cyan', levels=10)
save_figure('K(x,y)_streamlines', thumbnail=True)(fig)

The Kernel crashed while executing code in the current cell or a previous cell. 

Please review the code in the cell(s) to identify a possible cause of the failure. 

Click <a href='https://aka.ms/vscodeJupyterKernelCrash'>here</a> for more info. 

View Jupyter <a href='command:jupyter.viewOutput'>log</a> for further details.